In the picture shown below, you see a ladder with a length of four meters, placed against a wall. The ladder touches the box of one by one meter, which is standing against the wall.

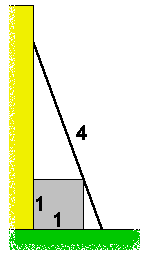
The question: At what height does the top of the ladder touch the wall?

The answer: Click here!