Here you see a square grid, on which we have selected five grid points (i.e., intersections of grid lines), numbered from 1 up to 5. We have also drawn the center points between each pair of these five points (shown in blue). As you can see, one of these center points (the center between points 2 and 5) is also exactly a grid point.

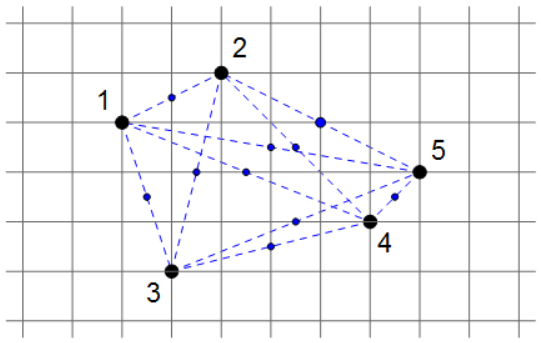
The question: Can you prove that whichever five grid points you select on a square grid, there are always at least two of those points of which the center point is also a grid point?

The answer: Click here!