Solution to: Leaning Ladder

The picture below shows the situation.

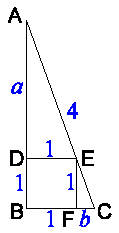
Let a be the length of line segment AD, and let b be the length of line segment CF.

Because of the similarity of the triangles ADE and EFC, the following holds:

a : 1 = 1 : b

so

ab = 1.

According to the Pythagorean Theorem, the following holds:

(AB)² + (BC)² = (AC)²

so

(a + 1)² + (1 + b)² = 4²

which can be rewritten to

a² + 2 + b² + 2(a + b) = 16.

Now we use the fact that ab = 1, so 2 = 2ab, and we get:

a² + 2ab + b² + 2(a + b) = 16

which can be rewritten to

(a + b)² + 2 × (a + b) - 16 = 0.

Because we know that a + b is greater than 0, using the quadratic formula we find that

a + b = √17 - 1.

Because of the similarity of the triangles ADE and EFC, the following holds:

a : 1 = 1 : b

so

b = 1 / a.

Now we know that

a + 1/a = √17 - 1

so

a² + (1 - √17) × a + 1 = 0.

We know that a is greater than 0, and using the quadratic formula we find the following two values for a:

½ × (√17 - 1 + √((1 - √17)² - 4)) ≈ 2.76
½ × (√17 - 1 - √((1 - √17)² - 4)) ≈ 0.36

The ladder touches the wall 1 meter higher, which is at about 3.76 or 1.36 meters. In the figure, we can see that only the answer 3.76 can be correct.

Conclusion: the ladder touches the wall at about 3.76 meters.

Back to the puzzle