Oplossing van: Leunende Ladder

De figuur hieronder geeft de situatie weer.

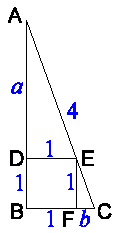
Laat a de lengte zijn van lijnstuk AD, en b de lengte van lijnstuk CF.

Door de gelijkvormigheid van driehoek ADE en driehoek EFC geldt dat

a : 1 = 1 : b

dus

ab = 1.

Volgens de stelling van Pythagoras geldt dat

(AB)² + (BC)² = (AC)²

dus

(a + 1)² + (1 + b)² = 4²

wat we kunnen herschrijven tot

a² + 2 + b² + 2(a + b) = 16.

Als we nu gebruikmaken van het feit dat ab = 1, dus 2 = 2ab, dan krijgen we:

a² + 2ab + b² + 2(a + b) = 16

wat we kunnen herschrijven tot

(a + b)² + 2 × (a + b) - 16 = 0.

Omdat we weten dat a + b groter is dan 0, kunnen we met behulp van de abc-formule vinden dat

a + b = √17 - 1.

Door de gelijkvormigheid van driehoek ADE en driehoek EFC geldt dat

a : 1 = 1 : b

dus

b = 1 / a.

We weten nu dat

a + 1/a = √17 - 1

dus

a² + (1 - √17) × a + 1 = 0.

We weten dat a groter is dan 0 en dus kunnen we met behulp van de abc-formule de volgende twee oplossingen voor a vinden:

½ × (√17 - 1 + √((1 - √17)² - 4)) ≈ 2,76
½ × (√17 - 1 - √((1 - √17)² - 4)) ≈ 0,36

De ladder komt nog 1 meter hoger, dus op ongeveer 3,76 of 1,36 meter. In het plaatje kunnen we echter zien dat alleen het antwoord 3,76 correct kan zijn.

Conclusie: de ladder raakt de muur op ongeveer 3,76 meter.

Terug naar de puzzel