Oplossing van: Kubus-Kruipers

We zullen de hoekpunten van de kubus met de volgende letters aanduiden:

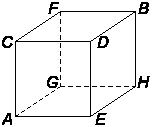
We geven de gemiddelde tijd (in jaren) die een kubuskruiper nog te leven heeft in een bepaald hoekpunt aan met dezelfde letter als het hoekpunt.

Als de kubuskruiper in punt B is gekomen, sterft hij. De gemiddelde tijd die het beestje nog te leven heeft in punt B is dus 0 jaar:

B = 0

Als de kubuskruiper in punt F zit, kan hij drie kanten op: naar punt B, C of G. Als hij naar punt B loopt, leeft hij nog 1 jaar. Als hij naar punt C loopt, leeft hij nog 1 jaar plus de gemiddelde tijd die hij nog te leven heeft in punt C. Als hij naar punt G loopt, leeft hij nog 1 jaar plus de gemiddelde tijd die hij nog te leven heeft in punt G. Elk van de drie richtingen heeft een gelijke kans om gekozen te worden, dus de kans is ¹⁄₃ voor elke richting. De gemiddelde tijd die het beestje nog te leven heeft als hij in punt F zit, is dus:

F = ¹⁄₃ × 1 + ¹⁄₃ × (1 + C) + ¹⁄₃ × (1 + G) = ¹⁄₃C + ¹⁄₃G + 1

Op dezelfde wijze kunnen we de tijd berekenen voor alle andere hoekpunten:

A = ¹⁄₃C + ¹⁄₃E + ¹⁄₃G + 1
C = ¹⁄₃A + ¹⁄₃D + ¹⁄₃F + 1
D = ¹⁄₃C + ¹⁄₃E + 1
E = ¹⁄₃A + ¹⁄₃D + ¹⁄₃H + 1
G = ¹⁄₃A + ¹⁄₃F + ¹⁄₃H + 1
H = ¹⁄₃E + ¹⁄₃G + 1

We beginnen nu met:

A = ¹⁄₃C + ¹⁄₃E + ¹⁄₃G + 1

en vullen daarin de formules voor C, E en G in:

A = ¹⁄₃ × (¹⁄₃A + ¹⁄₃D + ¹⁄₃F + 1) + ¹⁄₃ × (¹⁄₃A + ¹⁄₃D + ¹⁄₃H + 1) + ¹⁄₃ × (¹⁄₃A + ¹⁄₃F + ¹⁄₃H + 1) + 1

Dit kan herschreven worden tot:

A = ¹⁄₃A + ²⁄₉D + ²⁄₉F + ²⁄₉H + 2.

Nu vullen we de formules voor D, F en H in, wat resulteert in:

A = ¹⁄₃A + ⁴⁄₂₇C + ⁴⁄₂₇E + ⁴⁄₂₇G + ⁴⁄₉ + 2²⁄₉.

Omdat A = ¹⁄₃C + ¹⁄₃E + ¹⁄₃G + 1, is ⁴⁄₉A = ⁴⁄₂₇C + ⁴⁄₂₇E + ⁴⁄₂₇G + ⁴⁄₉. Als we dit invullen, krijgen we:

A = ¹⁄₃A + ⁴⁄₉A + 2²⁄₉

waaruit volgt dat A = 10. Kubuskruipers worden dus gemiddeld 10 jaar oud.

Terug naar de puzzel