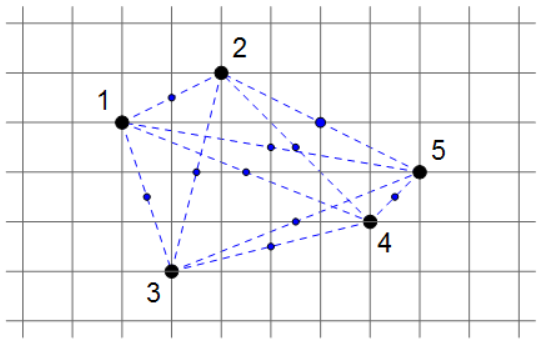
Hier siehst du ein quadratisches Gitternetz, auf dem wir fünf Gitterpunkte (das heißt, Schnittpunkte von Gitterlinien) ausgewählt haben, nummeriert von 1 bis 5. Wir haben auch die Mittelpunkte zwischen jedem Paar dieser fünf Punkte gezeichnet (in Blau dargestellt). Wie du sehen kannst, ist einer dieser Mittelpunkte (der Mittelpunkt zwischen den Punkten 2 und 5) ebenfalls ein Gitterpunkt.

Die Frage: Kannst du beweisen, dass egal welche fünf Gitterpunkte du auf einem quadratischen Gitter auswählst, es immer mindestens zwei dieser Punkte gibt, deren Mittelpunkt ebenfalls ein Gitterpunkt ist?

Die Lösung: Klick hier!