Lösung: Gewählte Gitterpunkte
Der erste Schritt ist, dass wir die Gitterlinien wie in einem mathematischen Gitternetz nummerieren, um die Koordinaten der fünf ausgewählten Punkte zu definieren. Für das Beispiel in der Frage kann dies wie in der untenstehenden Abbildung gezeigt erfolgen.
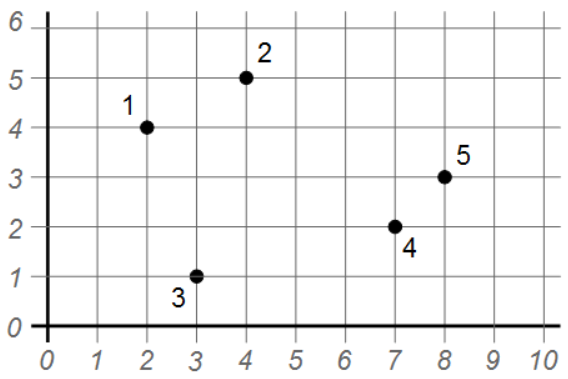
Jeder ausgewählte Gitterpunkt kann nun durch seine Koordinaten angegeben werden, unter Verwendung seiner horizontalen und vertikalen Liniennummer. Für das Beispiel in der Frage lauten die Koordinaten wie folgt:
| Punkt | Koordinaten |
|---|---|
| 1 | (2, 4) |
| 2 | (4, 5) |
| 3 | (3, 1) |
| 4 | (7, 2) |
| 5 | (8, 3) |
Der Mittelpunkt zwischen zwei Punkten kann berechnet werden, indem der Durchschnitt der Koordinaten genommen wird. Zum Beispiel hat der Mittelpunkt zwischen Punkt 1 (2, 4) und Punkt 2 (4, 5) die Koordinaten (3, 4½), was kein Gitterpunkt ist, und der Mittelpunkt zwischen Punkt 2 (4, 5) und Punkt 5 (8, 3) hat die Koordinaten (6, 4), was ein Gitterpunkt ist.
Der Mittelpunkt zwischen zwei Gitterpunkten ist auch ein Gitterpunkt, wenn sowohl der Unterschied zwischen den ersten Koordinaten als auch der Unterschied zwischen den zweiten Koordinaten gerade ist.
Daher platzieren wir die Koordinaten jedes ausgewählten Punktes in eine der folgenden vier Kategorien:
- (gerade, gerade)
- (gerade, ungerade)
- (ungerade, gerade)
- (ungerade, ungerade)
Der Mittelpunkt zwischen zwei Gitterpunkten ist auch ein Gitterpunkt, wenn die Koordinaten beider Punkte in derselben Kategorie sind. Für das Beispiel in der Frage liegen die Koordinaten der Punkte in den folgenden Kategorien:
| Punkt | Koordinaten | Kategorie |
|---|---|---|
| 1 | (2, 4) | (gerade, gerade) |
| 2 | (4, 5) | (gerade, ungerade) |
| 3 | (3, 1) | (ungerade, ungerade) |
| 4 | (7, 2) | (ungerade, gerade) |
| 5 | (8, 3) | (gerade, ungerade) |
Wie du sehen kannst, sind die Punkte 2 und 5 in derselben Kategorie (gerade, ungerade). Der Mittelpunkt zwischen diesen beiden Gitterpunkten ist (6, 4), was ein Gitterpunkt ist.
Da es fünf Punkte und nur vier Kategorien gibt, können wir das Schubfachprinzip anwenden. Das Schubfachprinzip besagt, dass wenn du Objekte auf Mengen verteilst und es mehr Objekte als Mengen gibt, mindestens eine Menge zwei oder mehr Objekte enthalten wird.
In unserem Fall muss es mindestens eine Kategorie geben, die zwei oder mehr Punkte enthält. Das bedeutet, dass egal welche fünf Gitterpunkte du auf einem quadratischen Gitter auswählst, es immer mindestens zwei dieser Punkte gibt, dener Mittelpunkt ebenfalls ein Gitterpunkt ist.