Twelve matchsticks form four equal squares.

The question: How can exactly four matchsticks be moved to make three equal squares?

The solution: Click here!

Another question: Twelve matchsticks form four equal squares.

How can exactly three matchsticks be moved to make three equal squares?

Another solution: Click here!

Yet another question: Sixteen matchsticks form five squares.

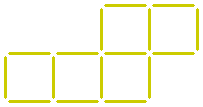
Can you make four squares from this by moving two matchsticks?

Yet another solution: Click here!

The fourth question: Sixteen matchsticks form five squares.

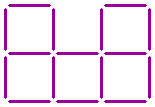
Can you turn these five squares into four squares by moving three matchsticks?

The fourth solution: Click here!

The fifth question: Twenty matchsticks form seven equal squares.

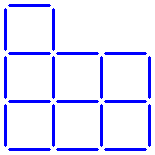
How can three matchsticks be moved to make five equal squares?

The fifth solution: Click here!

The sixth question: By moving only two matchsticks, these three equal sized squares can be changed into four equal sized rectangles.

How can this be done?

The sixth solution: Click here!

The seventh question: Here you see two squares. Can you form three squares by moving four matchsticks?

The seventh solution: Click here!

The eighth question: The figure below contains five squares (four small ones and a large one). Can you form seven squares by moving just two matchsticks, without having overlapping matchsticks?

The eighth solution: Click here!

The ninth question: The figure below contains five squares (four small ones and a large one). Can you form ten squares by moving just four matchsticks?

The ninth solution: Click here!