Lösung: Männer auf den Mond

Aus dem ersten Teil dieses Rätsels wissen wir, dass der Radius eines Kreises, der gleich der Länge des Kabels ist, 1/(2 × π) Meter weniger ist als der Radius des Mondes. Deswegen ist in der untenstehenden Figur

x = r - 1/(2 × π)

und

cos(a) = x / r = (r - 1/(2 × π) ) / r

Wenn wir a in Radianten nehmen, gilt:

y = (a / (2 × π) ) × (2 × π × r) = a × r.

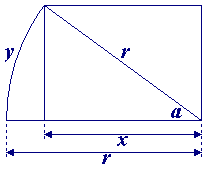
Da r=3476000/2=1738000 Meter, können wir berechnen, dass y ungefähr 744 Meter ist, was der Abstand ist, um den das Kabel nördlich des Äquators des Mondes verlegt werden muss, wenn man das Defizit von 1 Meter überwinden will.

Zurück zum Rätsel