Lösung: Lehnende Leiter

Die untenstehende Figur rechts stellt die Lage dar.

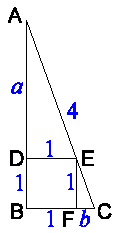
Sei a die Länge der Linie AD und b die Länge der Linie CF.

Wegen der Ähnlichkeit der Dreiecke ADE und EFC gilt, dass:

a : 1 = 1 : b

Also gilt:

ab = 1.

Laut des pythagoreischen Lehrsatzes gilt, dass

(AB)² + (BC)² = (AC)²

Also:

(a + 1)² + (1 + b)² = 4²

was wir umschreiben können zu:

a² + 2 + b² + 2(a + b) = 16.

Wenn wir jetzt Gebrauch machen von der Tatsache ab = 1, also 2 = 2ab, dann bekommen wir:

a² + 2ab + b² + 2(a + b) = 16

was wir umschreiben können zu:

(a + b)² + 2 × (a + b) - 16 = 0.

Weil wir wissen, dass a + b größer ist als 0, können wir mit Hilfe der a-b-c-Formel (Mitternachtsformel) finden, dass

a + b = √17 - 1.

Wegen der Ähnlichkeit der Dreiecke ADE und EFC gilt, dass:

a : 1 = 1 : b

Also gilt:

b = 1 / a.

Wir wissen jetzt, dass

a + 1/a = √17 - 1

also:

a² + (1 - √17) × a + 1 = 0.

Wir wissen, dass a größer ist als 0, und deswegen können wir mit Hilfe der a-b-c-Formel die folgenden zwei Lösungen für a finden:

½ × (√17 - 1 + √((1 - √17)² - 4)) ≈ 2,76
½ × (√17 - 1 - √((1 - √17)² - 4)) ≈ 0,36

Die Leiter kommt noch 1 Meter höher, also circa 3,76 oder 1,36 Meter. In der Figur können wir aber sehen, dass nur die Antwort 3,76 korrekt sein kann.

Konklusion: Die Leiter berührt die Mauer auf circa 3,76 Metern.

Zurück zum Rätsel