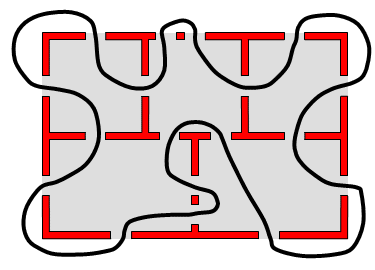
Lösung: Zugängliche Zimmer

Du wirst wahrscheinlich bemerkt haben, dass du, egal wie du auch gehst, immer mindestens eine Tür übrig lässt! Es zeigt sich, dass es unmöglich ist, einen Spaziergang durch alle Zimmer zu machen und dabei genau einmal durch jede Tür zu gehen. Der Beweis findest du hier unten.

Wir betrachten den Raum außerhalb des Hauses auch als ein Zimmer. Also gibt es insgesamt sechs Zimmer. Nimm an, dass du einen Spaziergang machst und dabei genau einmal durch jede Tür gehst.

Du gehst aus dem ersten Zimmer. Du gehst in das nächste Zimmer und wieder aus diesem Zimmer. Du gehst in das nächste Zimmer und wieder aus diesem Zimmer, und so weiter, bis zum letzten Zimmer, in welches du nur eingehst.

Lass uns mal zählen, wie oft du in ein Zimmer ein- und ausgehst. Jedes Zimmer, in dem du nicht anfängst und endest, betrittst du gleich oft ein und aus. Deshalb müssen diese Zimmer eine gerade Anzahl an Türen haben.

Wenn du in demselben Zimmer anfängst und endest, dann gehst du auch in dieses Zimmer gleich oft ein und aus. Also ist auch die Zahl der Türen dieses Zimmers dann gerade.

Wenn du in verschiedenen Zimmern anfängst und endest, dann gehst du das erste Zimmer einmal öfter aus und das letzte Zimmer einmal öfter ein. Also müssen diese Zimmer dann eine ungerade Anzahl an Türen haben.

Zusammengefasst: Wenn es möglich wäre, einen Spaziergang durch alle Zimmer zu machen und dabei genau einmal durch jede Tür zu gehen, dann muss eine der folgenden zwei Situationen gelten:

• alle Zimmer haben eine gerade Anzahl an Türen, oder
• genau zwei Zimmer haben eine ungerade Anzahl an Türen.

Es gibt jedoch vier Zimmer mit einer ungeraden Anzahl an Türen (drei Zimmer im Haus und der Raum außerhalb des Hauses, den wir auch als ein Zimmer betrachten). Konklusion: Es ist nicht möglich, einem Spaziergang durch alle Zimmer zu machen und dabei genau einmal durch jede Tür zu gehen.

Nur wenn wir dafür sorgen, dass nur zwei Zimmer eine ungerade Anzahl an Türen haben, zum Beispiel wenn man eine Tür hinzufügt, ist es möglich, einen Spaziergang durch alle Zimmer zu machen und dabei genau einmal durch jede Tür zu gehen. In der Abbildung hier unten haben nur ein Zimmer und der Raum außerhalb des Hauses eine ungerade Anzahl an Türen.

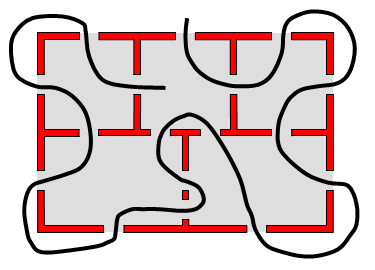
Wenn wir dafür sorgen, dass alle Zimmer eine gerade Anzahl an Türen haben, zum Beispiel wenn man noch eine Tür hinzufügt, ist es möglich, einen ganzen Rundgang durch alle Zimmer zu machen (wobei man in demselben Zimmer anfängt und endet):

Zurück zum Rätsel