Solution to: Cube Crawlers

We shall refer to the vertices of the cube with the following letters:

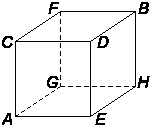
We shall denote the average time (in years) that a cube crawler has left to live at a certain vertex with the same letter as the vertex itself.

If the cube crawler arrives in point B, it dies. The average time that the animal has left to live in point B is therefore 0 years:

B = 0

If the cube crawler is in point F, it can go in three directions: to points B, C, or G. If it walks to point B, it has 1 year left to live. If it walks to point C, it has 1 year plus the average time it has left to live in point C. If it walks to point G, it has 1 year plus the average time it has left to live in point G. Each of the three directions has an equal probability of being chosen, so the probability for each direction is ¹⁄₃. The average time that the cube crawler has left to live when it is at point F is therefore:

F = ¹⁄₃ × 1 + ¹⁄₃ × (1 + C) + ¹⁄₃ × (1 + G) = ¹⁄₃C + ¹⁄₃G + 1

In the same way, we can calculate the time left to live for all other vertices:

A = ¹⁄₃C + ¹⁄₃E + ¹⁄₃G + 1
C = ¹⁄₃A + ¹⁄₃D + ¹⁄₃F + 1
D = ¹⁄₃C + ¹⁄₃E + 1
E = ¹⁄₃A + ¹⁄₃D + ¹⁄₃H + 1
G = ¹⁄₃A + ¹⁄₃F + ¹⁄₃H + 1
H = ¹⁄₃E + ¹⁄₃G + 1

Now we start with:

A = ¹⁄₃C + ¹⁄₃E + ¹⁄₃G + 1

and substitute the formulas for C, E, and G:

A = ¹⁄₃ × (¹⁄₃A + ¹⁄₃D + ¹⁄₃F + 1) + ¹⁄₃ × (¹⁄₃A + ¹⁄₃D + ¹⁄₃H + 1) + ¹⁄₃ × (¹⁄₃A + ¹⁄₃F + ¹⁄₃H + 1) + 1

This can be rewritten as:

A = ¹⁄₃A + ²⁄₉D + ²⁄₉F + ²⁄₉H + 2.

Now we substitute the formulas for D, F, and H, which results in:

A = ¹⁄₃A + ⁴⁄₂₇C + ⁴⁄₂₇E + ⁴⁄₂₇G + ⁴⁄₉ + 2²⁄₉.

Since A = ¹⁄₃C + ¹⁄₃E + ¹⁄₃G + 1, it also follows that ⁴⁄₉A = ⁴⁄₂₇C + ⁴⁄₂₇E + ⁴⁄₂₇G + ⁴⁄₉. If we substitute this in, we get:

A = ¹⁄₃A + ⁴⁄₉A + 2²⁄₉

From this, it follows that A = 10. Conclusion: Cube crawlers live for an average of 10 years.

Back to the puzzle