Lösung: Kubus-Kriecher
Wir werden die Ecken des Würfels mit den folgenden Buchstaben bezeichnen:
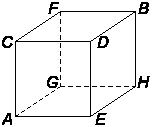
Wir geben die durchschnittliche Zeit (in Jahren), die ein Kubuskriecher an einem bestimmten Eckpunkt noch zu leben hat, mit demselben Buchstaben wie dem Eckpunkt an.
Wenn der Kubuskriecher in Punkt B angekommen ist, stirbt es. Die durchschnittliche Zeit, die das Tier in Punkt B noch zu leben hat, ist also 0 Jahre:
B = 0
Wenn der Kubuskriecher in Punkt F ist, kann er in drei Richtungen gehen: zu Punkt B, C oder G. Wenn er zu Punkt B geht, lebt er noch 1 Jahr. Wenn er zu Punkt C geht, lebt er noch 1 Jahr plus die durchschnittliche Zeit, die er in Punkt C noch zu leben hat. Wenn er zu Punkt G geht, lebt er noch 1 Jahr plus die durchschnittliche Zeit, die er in Punkt G noch zu leben hat. Jede der drei Richtungen hat die gleiche Wahrscheinlichkeit, gewählt zu werden, also ist die Wahrscheinlichkeit 1⁄3 für jede Richtung. Die durchschnittliche Zeit, die das Tierchen noch zu leben hat, wenn es in Punkt F ist, ist also:
F = 1⁄3 × 1 + 1⁄3 × (1 + C) + 1⁄3 × (1 + G) = 1⁄3C + 1⁄3G + 1
Auf die gleiche Weise können wir die Zeit für alle anderen Eckpunkte berechnen:
A = 1⁄3C + 1⁄3E + 1⁄3G + 1
C = 1⁄3A + 1⁄3D + 1⁄3F + 1
D = 1⁄3C + 1⁄3E + 1
E = 1⁄3A + 1⁄3D + 1⁄3H + 1
G = 1⁄3A + 1⁄3F + 1⁄3H + 1
H = 1⁄3E + 1⁄3G + 1
Wir beginnen nun mit:
A = 1⁄3C + 1⁄3E + 1⁄3G + 1
und setzen die Formeln für C, E und G ein:
A = 1⁄3 × (1⁄3A + 1⁄3D + 1⁄3F + 1) + 1⁄3 × (1⁄3A + 1⁄3D + 1⁄3H + 1) + 1⁄3 × (1⁄3A + 1⁄3F + 1⁄3H + 1) + 1
Das kann umgeschrieben werden zu:
A = 1⁄3A + 2⁄9D + 2⁄9F + 2⁄9H + 2.
Jetzt setzen wir die Formeln für D, F und H ein, was zu folgendem Ergebnis führt:
A = 1⁄3A + 4⁄27C + 4⁄27E + 4⁄27G + 4⁄9 + 22⁄9.
Da A = 1⁄3C + 1⁄3E + 1⁄3G + 1, gilt 4⁄9A = 4⁄27C + 4⁄27E + 4⁄27G + 4⁄9. Wenn wir dies einsetzen, erhalten wir:
A = 1⁄3A + 4⁄9A + 22⁄9
woraus folgt, dass A = 10. Fazit: Kubuskriecher werden im Durchschnitt 10 Jahre alt.