Verschiedene Formen ★★
Es gibt vier Quadrate in der untenstehenden Figur.
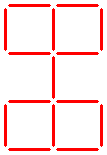
![]() Die Frage:
Kannst du zwei Streichhölzer umlegen, sodass fünf Quadrate entstehen?
Die Frage:
Kannst du zwei Streichhölzer umlegen, sodass fünf Quadrate entstehen?
![]() Die Lösung:
Klick hier!
Die Lösung:
Klick hier!
![]() Noch eine Frage:
Die sechs untenstehenden Streichhölzer bilden ein Sechseck.
Noch eine Frage:
Die sechs untenstehenden Streichhölzer bilden ein Sechseck.
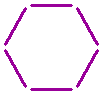
Kannst du dieses Sechseck in zwei Rauten verwandeln, wenn du nur zwei Streichhölzer umlegen und ein Streichholz hinzufügen darfst?
![]() Noch eine Lösung:
Klick hier!
Noch eine Lösung:
Klick hier!
![]() Und noch eine Frage:
Kannst du in der untenstehenden Figur genau vier Streichhölzer umlegen, sodass vier identische Dreiecke entstehen?
Und noch eine Frage:
Kannst du in der untenstehenden Figur genau vier Streichhölzer umlegen, sodass vier identische Dreiecke entstehen?

![]() Und noch eine Lösung:
Klick hier!
Und noch eine Lösung:
Klick hier!
![]() Die vierte Frage:
Zwölf Streichhölzer bilden ein Quadrat und vier Dreiecke.
Die vierte Frage:
Zwölf Streichhölzer bilden ein Quadrat und vier Dreiecke.
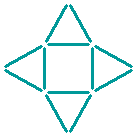
Kannst du sechs Streichhölzer umlegen, sodass drei Quadrate und ein Dreieck entstehen?
![]() Die vierte Lösung:
Klick hier!
Die vierte Lösung:
Klick hier!
![]() Die fünfte Frage:
Kannst du vier Streichhölzer umlegen, sodass zwei Quadrate entstehen?
Die fünfte Frage:
Kannst du vier Streichhölzer umlegen, sodass zwei Quadrate entstehen?
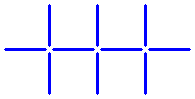
![]() Die fünfte Lösung:
Klick hier!
Die fünfte Lösung:
Klick hier!
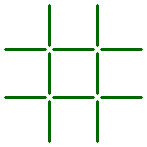
![]() Die sechste Frage:
Kannst du in der untenstehenden Figur nur drei Streichhölzer umlegen, sodass drei gleich große Quadrate entstehen?
Die sechste Frage:
Kannst du in der untenstehenden Figur nur drei Streichhölzer umlegen, sodass drei gleich große Quadrate entstehen?
![]() Die sechste Lösung:
Klick hier!
Die sechste Lösung:
Klick hier!
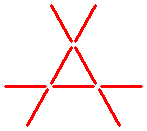
![]() Die siebte Frage:
Kannst du in der untenstehenden Figur genau drei Streichhölzer umlegen, sodass drei Dreiecke entstehen, die einander berühren?
Die siebte Frage:
Kannst du in der untenstehenden Figur genau drei Streichhölzer umlegen, sodass drei Dreiecke entstehen, die einander berühren?
![]() Die siebte Lösung:
Klick hier!
Die siebte Lösung:
Klick hier!
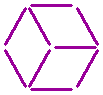
![]() Die achte Frage:
Kannst du in der untenstehenden Figur drei Streichhölzer umlegen, sodass drei Dreiecke entstehen?
Die achte Frage:
Kannst du in der untenstehenden Figur drei Streichhölzer umlegen, sodass drei Dreiecke entstehen?
![]() Die achte Lösung:
Klick hier!
Die achte Lösung:
Klick hier!