Quadrate Formen ★★
Zwölf Streichhölzer bilden vier identische Quadrate.

![]() Die Frage:
Kannst du genau vier Streichhölzer umlegen, sodass drei identische Quadrate entstehen?
Die Frage:
Kannst du genau vier Streichhölzer umlegen, sodass drei identische Quadrate entstehen?
![]() Die Lösung:
Klick hier!
Die Lösung:
Klick hier!
![]() Noch eine Frage:
Zwölf Streichhölzer bilden vier identische Quadrate.
Noch eine Frage:
Zwölf Streichhölzer bilden vier identische Quadrate.

Kannst du genau drei Streichhölzer umlegen, sodass drei identische Quadrate entstehen?
![]() Noch eine Lösung:
Klick hier!
Noch eine Lösung:
Klick hier!
![]() Und noch eine Frage:
Sechzehn Streichhölzer bilden fünf Quadrate.
Und noch eine Frage:
Sechzehn Streichhölzer bilden fünf Quadrate.
Kannst du zwei Streichhölzer umlegen, sodass vier identische Quadrate entstehen?
![]() Und noch eine Lösung:
Klick hier!
Und noch eine Lösung:
Klick hier!
![]() Die vierte Frage:
Sechzehn Streichhölzer bilden fünf Quadrate.
Die vierte Frage:
Sechzehn Streichhölzer bilden fünf Quadrate.
Kannst du drei Streichhölzer umlegen, sodass vier identische Quadrate entstehen?
![]() Die vierte Lösung:
Klick hier!
Die vierte Lösung:
Klick hier!
![]() Die fünfte Frage:
Zwanzig Streichhölzer bilden sieben identische Quadrate.
Die fünfte Frage:
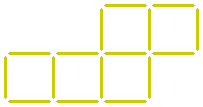
Zwanzig Streichhölzer bilden sieben identische Quadrate.
Kannst du genau drei Streichhölzer umlegen, sodass fünf identische Quadrate entstehen?
![]() Die fünfte Lösung:
Klick hier!
Die fünfte Lösung:
Klick hier!
![]() Die sechste Frage:
Wenn man nur zwei Streichhölzer umlegt, kann man die drei untenstehenden Quadrate in vier identische Rechtecke verwandeln.
Die sechste Frage:
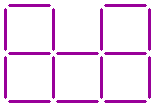
Wenn man nur zwei Streichhölzer umlegt, kann man die drei untenstehenden Quadrate in vier identische Rechtecke verwandeln.

Wie kann man das machen?
![]() Die sechste Lösung:
Klick hier!
Die sechste Lösung:
Klick hier!
![]() Die siebte Frage:
Hier siehst du zwei Quadrate.
Kannst du vier Streichhölzer umlegen, sodass drei Quadrate entstehen?
Die siebte Frage:
Hier siehst du zwei Quadrate.
Kannst du vier Streichhölzer umlegen, sodass drei Quadrate entstehen?

![]() Die siebte Lösung:
Klick hier!
Die siebte Lösung:
Klick hier!
![]() Die achte Frage:
Es gibt fünf Quadrate in der untenstehenden Figur (vier kleine und ein großes).
Kannst du zwei Streichhölzer umlegen, sodass sieben Quadrate entstehen, ohne sich überlappende Streichhölzer?
Die achte Frage:
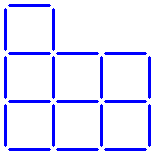
Es gibt fünf Quadrate in der untenstehenden Figur (vier kleine und ein großes).
Kannst du zwei Streichhölzer umlegen, sodass sieben Quadrate entstehen, ohne sich überlappende Streichhölzer?

![]() Die achte Lösung:
Klick hier!
Die achte Lösung:
Klick hier!
![]() Die neunte Frage:
Es gibt fünf Quadrate in der untenstehenden Figur (vier kleine und ein großes).
Kannst du vier Streichhölzer umlegen, sodass zehn Quadrate entstehen?
Die neunte Frage:
Es gibt fünf Quadrate in der untenstehenden Figur (vier kleine und ein großes).
Kannst du vier Streichhölzer umlegen, sodass zehn Quadrate entstehen?

![]() Die neunte Lösung:
Klick hier!
Die neunte Lösung:
Klick hier!