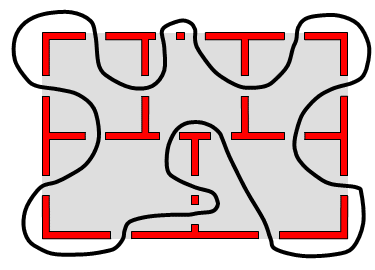
Solution to: Running through the Rooms
You will have noticed that, whatever route you try, there will always be at least one door left over! It turns out that it is impossible to make a run through the rooms and pass each of the sixteen doors exactly once. You can find the proof for this below.
For the sake of reasoning, let us consider the outside world to be a room as well. Consequently, there are six rooms in total. Now, assume you make a run where you pass each door exactly once.
You leave the room where you started. You enter the next room and leave it again. The next room you enter and leave again, etcetera. Until the last room, which you only enter.
Let us have a look at the number of times you entered and left a room. For rooms in which you neither start nor finish, the number of enters and leaves is equal. Therefore, those rooms must have an even number of doors.
If you start in the same room as you finish, then also the number of enters and leaves is equal for that room. Therefore, the number of doors is even.
If you start in a different room from the one you finish, then you will leave the starting room once more than you enter it, and you will enter the finishing room once more than you leave it. Consequently, these two rooms must have an odd number of doors.
Summarizing, if there would exist a run through the rooms where you pass each door exactly once then either of the following two situations hold:
- All rooms have an even number of doors.
- Exactly two rooms have an odd number of doors.
However, there are four rooms with an odd number of doors (three rooms in the house, and the outside world, which we consider a room as well). Conclusion: it is impossible to make a run where you pass each door exactly once.
Only if we make sure that just two rooms have an odd number of doors, for instance by adding a door in the house, it is possible to make a complete run through the house and pass each door exactly once. In the drawing below only one room and the outside world have an odd number of doors:
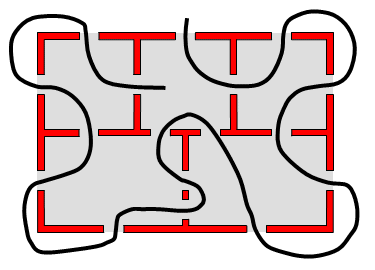
If we make sure that all rooms have an even number of doors, by for instance adding another door, a complete round trip becomes possible (as the trip will start and finish in the same room):