Solution to: Ladder Alley
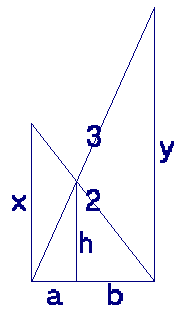
Define the following variables (see the figure below):
- x is the height at which the ladder of 2 meters touches the wall of the alley;
- y is the height at which the ladder of 3 meters touches the wall of the alley;
- a is the horizontal distance between the point where the ladders cross and the wall to which the ladder of 2 meters is standing;
- b is the horizontal distance between the point where the ladders cross and the wall to which the ladder of 3 meters is standing;
- w is the width of the alley (equals a+b);
- h is the height at which the ladders cross (1 meter).
Because of the similarity of triangles,
x / w = h / b
and
y / w = h / a
so
b = (w × h) / x
and
a = (w × h) / y.
Combining this with
a + b = w
gives
(w × h) / y+(w × h) / x = w
from which it follows that
h × x + h × y = x × y
from which we conclude that
y = (h × x) / (x - h).
Because of Pythagoras' theorem,
w = sqrt(32 - y2) = sqrt(9 - y2)
and
w = sqrt(22 - x2) = sqrt(4 - x2).
Combining these two equations gives
9 - y2 = 4 - x2
so
y2 - x2 = 5.
Combining this with
y = (h × x) / (x - h)
and h = 1, results in:
(x / (x - 1))2 - x2 = 5.
Solving this equation gives:
x = 1/2 + (sqrt(c) + sqrt((24 × sqrt(2) / sqrt(c)) - c -14)) / (2 × sqrt(2))
where
c = 2 × (d + (25 / d) - 7) / 3
and
d = (395 + 60 × sqrt(39))1/3.
Since w = sqrt(4 - x2), this gives 1.231185724... meters for the width of the alley.
It is interesting to note that there are combinations of integer ladder lengths and an integer crossing height, for which the width of the alley is also an integer value. The combination with the smallest values for which this is the case, is the following one:
- shortest ladder: 70,
- longest ladder: 119,
- crossing height: 30,
- width of the alley: 56.